Distributed Relational Learning
Learning from relational data, in which entities can be connected to each other with varying types of relations (friendOf, worksFor, …), frustrates many machine learning algorithms which expect tabular data. How do you represent all the friends of an individual in a table? One method is to have a column for every person, with a 1 indicating that the associated person is a friend, and a 0 if not. This leads to very large, but sparse matrices. Another approach is to learn latent, compact representations of the entities which somehow capture the relationships the entity is involved in, and encodes this data as a point in n-dimensional space (n usually being “smallish”, up to hundreds or thousands, but regularly only in the tens).
In the past few months, GA-CCRi has developed distributed software to train models which learn such embeddings for data described by RDF. The models we apply are inspired by Bordes, et al. in [1], and our distributed approach is in line with the approaches of Hogwild! [2] and DistBelief [3].
The models we develop embed entities (subject or object of an RDF triple) in vector space, and let relations correspond to linear translations of the space. This means that all entities and relations can be represented with the same width vector, which is convenient. Abusing notation, slightly, if (s,p,o) is a triple in the data, we hope for our model to learn embeddings so that s+p is “close to” o. More specifically, we want o to be closer to s+p than any other entity which is not, also, the object of a triple of the form (s,p,x).
Stochastic gradient descent is used to update the coordinates of entities, and the translations corresponding to relations, to best model the training data. We adapt this to a distributed setting, where multiple clients retrieve and update parameter values concurrently, as justified by [2] and [3] and our own subsequent results. Since we adopt this framework, we make a minor tweak to the model of Bordes. Namely, we no longer assume, as in that paper, that entities are constrained to lie on a hypersphere. Instead, we apply a traditional regularization penalty, computed for each training batch. This allows us to simply post updates and not have to worry about when to normalize our entity coordinates, and we have validated that the models we produce are at least as effective as the original models.
A unique capability of our implementation is that training can be distributed to multiple clients acting concurrently, and each can actually operate on a different subset of the data. We have found that by splitting a dataset, and using two clients to train a common model on their partitions of the input triples, we can actually train a better model in the same amount of time. It seems that the more triples that are common to the clients the better, though, as two clients, each with access to the full dataset, did even better in the same amount of time.
We should say, of course, that “better” here means the ability to infer held-out triples. If (s,p,o) is a triple that is held out of training, we can evaluate how well the model predicts it by calculating the distance from s+p to e, for all entities e. The number of entities which are closer to s+p than o is to s+p is the rank of the “correct” answer, o, and the score of the model on this held-out test triple. Note, of course, that we could also predict for the subject just as easily. The ability to predict missing links in a relational dataset is a challenging problem, and the models we describe above are an effective method for attacking it.
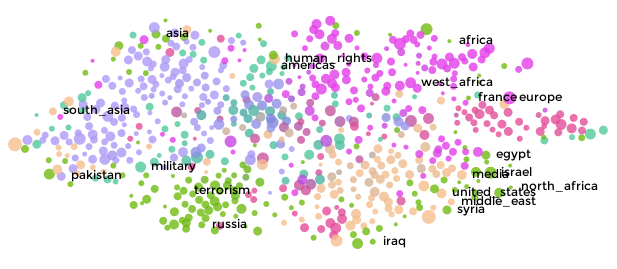
Finally, the embeddings we learn can be used for additional machine learning, besides predicting relationships, as was our original motivation. GA-CCRi has implemented advanced dimensionality reduction procedures so that we can visualize relationships between entities in large triple stores quickly and efficiently. The user interface we have developed is called Mantis, whose developer, Tim, will describe it in more detail in the next post. For now, I’ll offer up a teaser:
References:
- [1] Bordes, Antoine, et al. “Translating embeddings for modeling multi-relational data.” Advances in Neural Information Processing Systems. 2013.
- [2] Niu, Feng, et al. “Hogwild!: A lock-free approach to parallelizing stochastic gradient descent.” Advances in Neural Information Processing Systems 24 (2011): 693-701.
- [3] Dean, Jeffrey, et al. “Large Scale Distributed Deep Networks.” NIPS. 2012.