GA-CCRi Analytical Development Services

TransE, or Translating Embeddings for Modeling Multi-relational Data, lets us embed the contents of a knowledge graph by assigning vectors to nodes and edge types (a.k.a. predicates) and, for each subject-predicate-object triple, minimizing the distance between the object vector and the translation of the subject vector along the predicate vector. It’s an appealing algorithm for embedding multi-relational data due to its simplicity, efficiency, and quality. However, it can sometimes behave in mysterious and counter-intuitive ways.

To try to isolate and unravel some of these issues, I ran TransE in two dimensions for several small graphs. The advantage of this approach is that we can visualize and animate the whole graph during training to gain intuition for how TransE works. I also plotted the predicate vectors separately to give us a good view of how they change over time. In the examples below, the entity embeddings along with the graph edges appear on the left plot and the predicate vectors appear on the right plot.

Path graph

Paths are probably the simplest possible family of graphs, and they are obviously well-suited to translational embeddings. No surprises here; TransE lays out the graph perfectly, with each edge aligned with the predicate vector:

Path graph (two predicates)

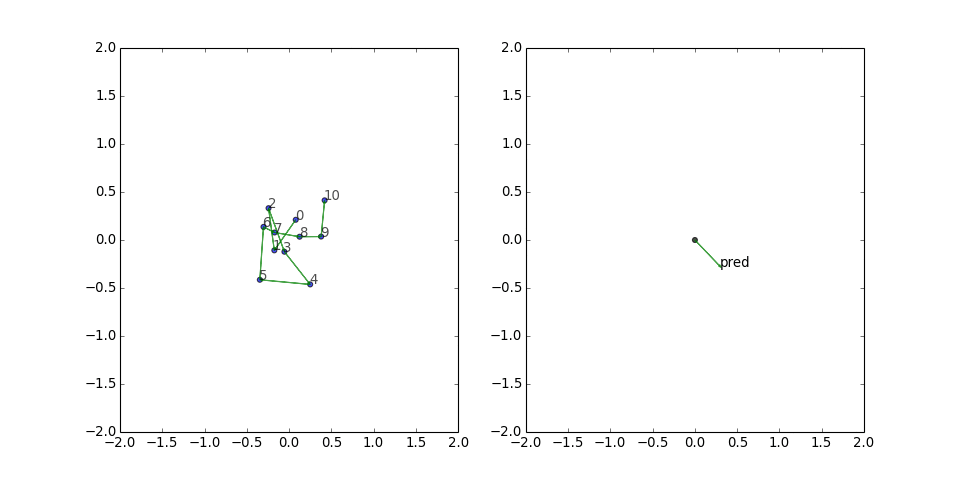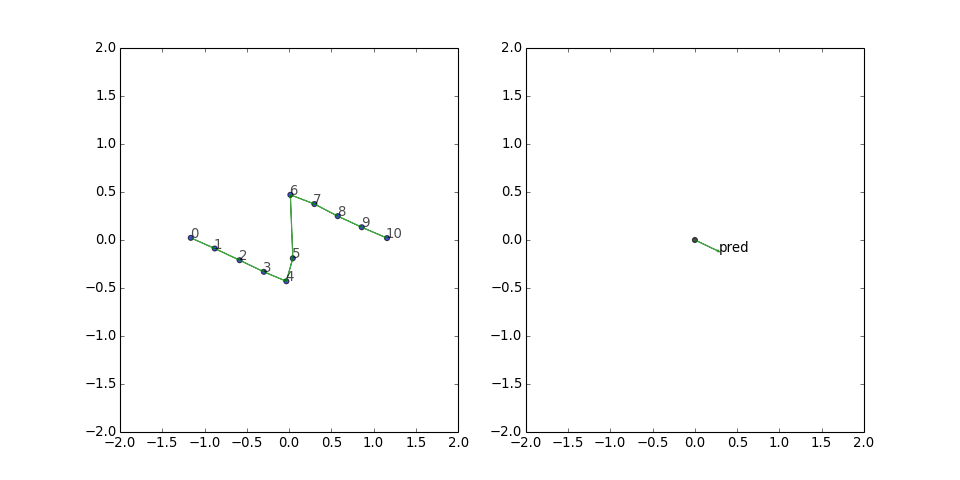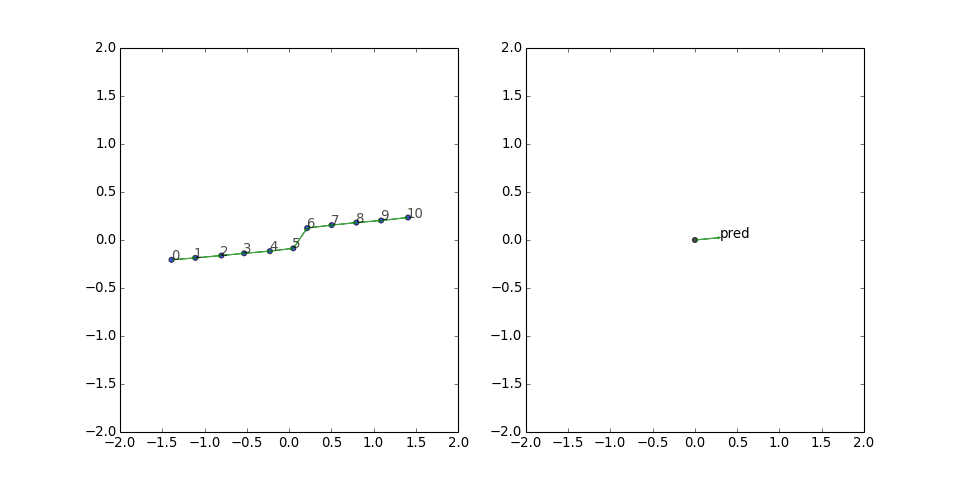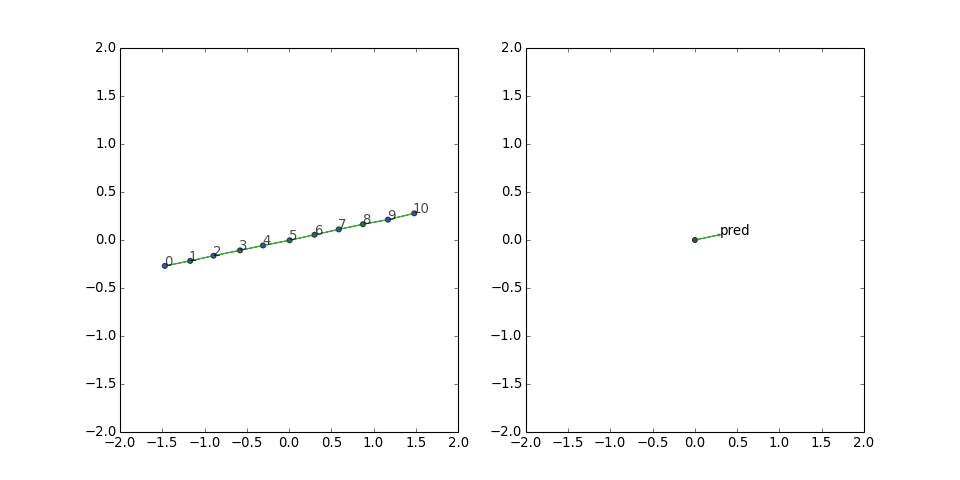
Next, I tried a path graph with two distinct predicates alternating along the path. Again, TransE lays out the path vertices in order, with each edge aligned perfectly with its corresponding predicate vector:

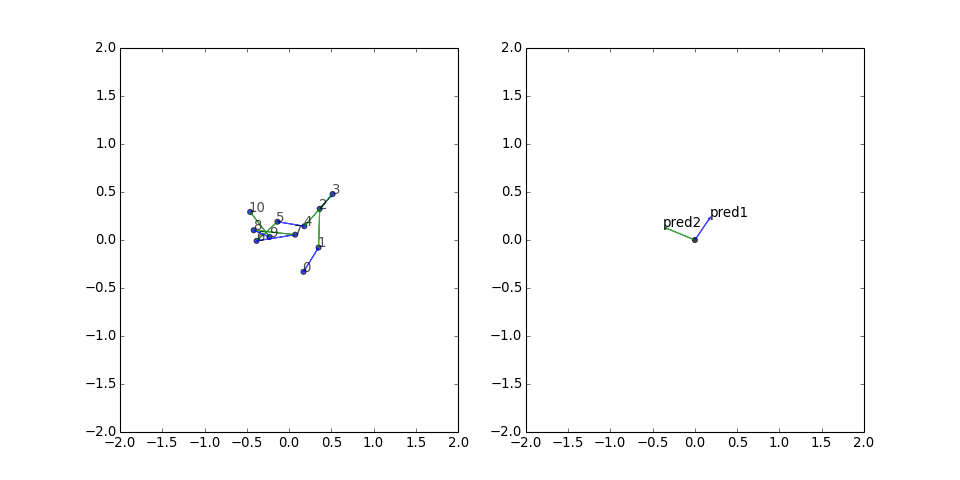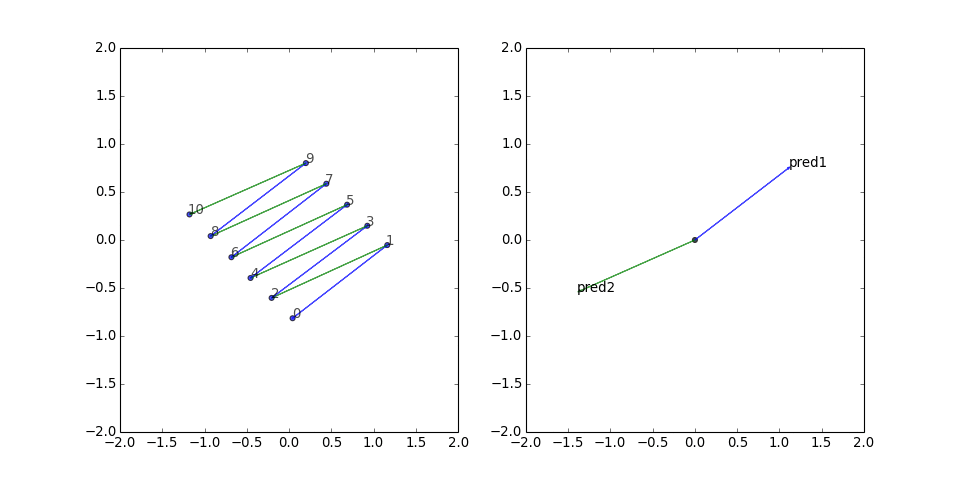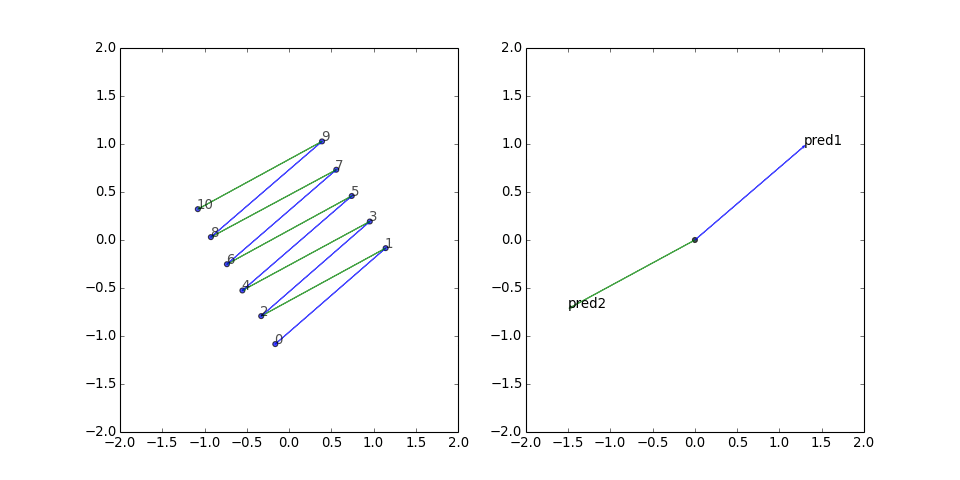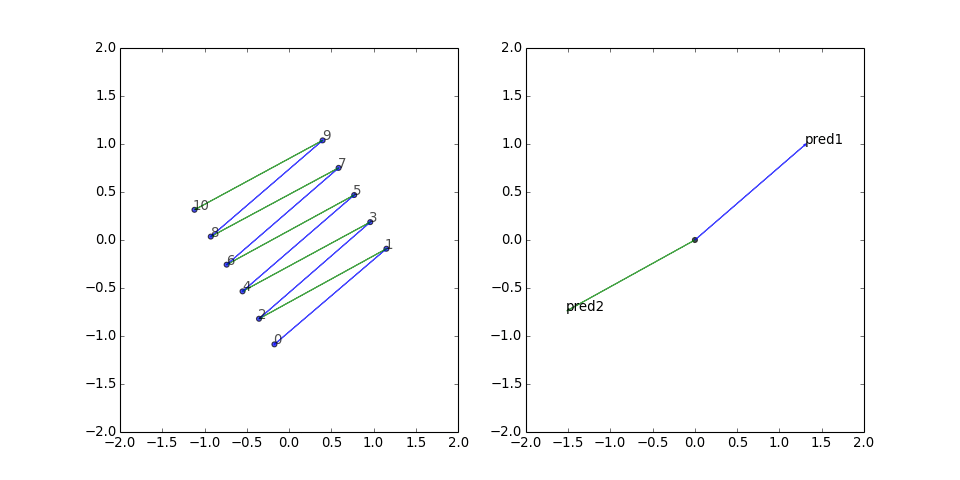
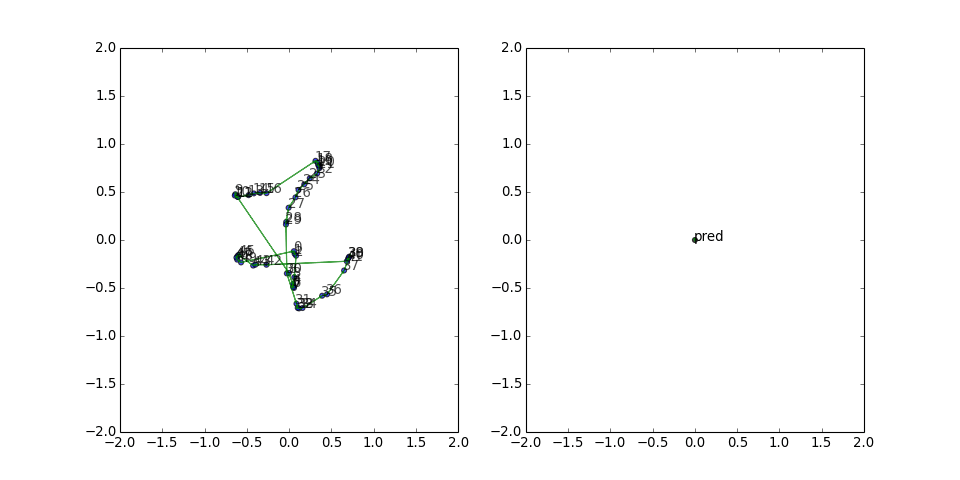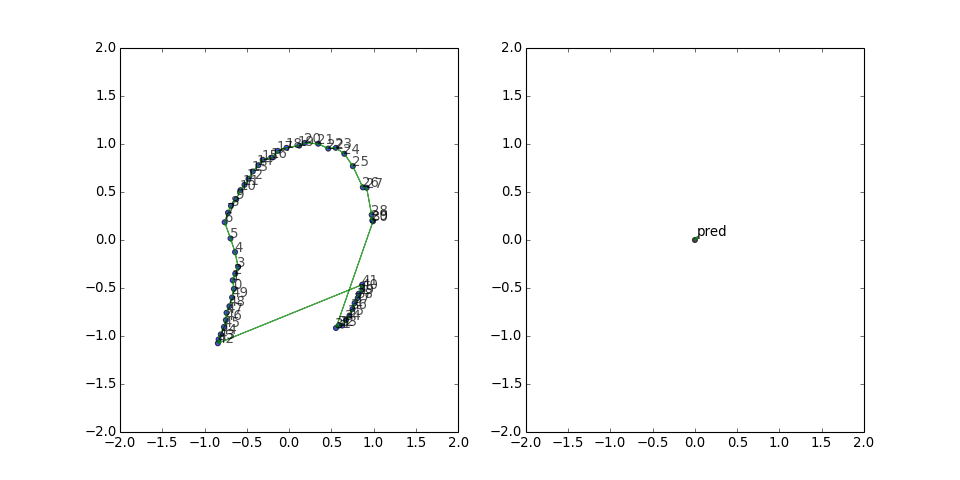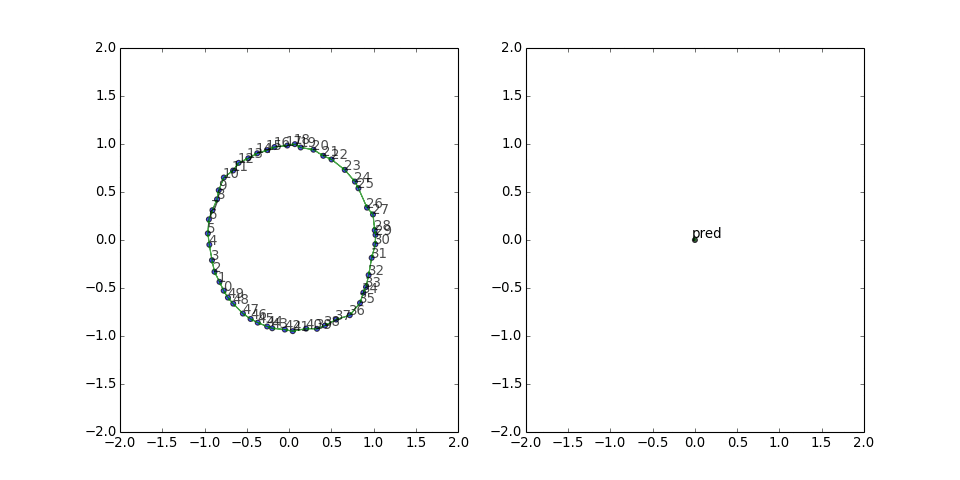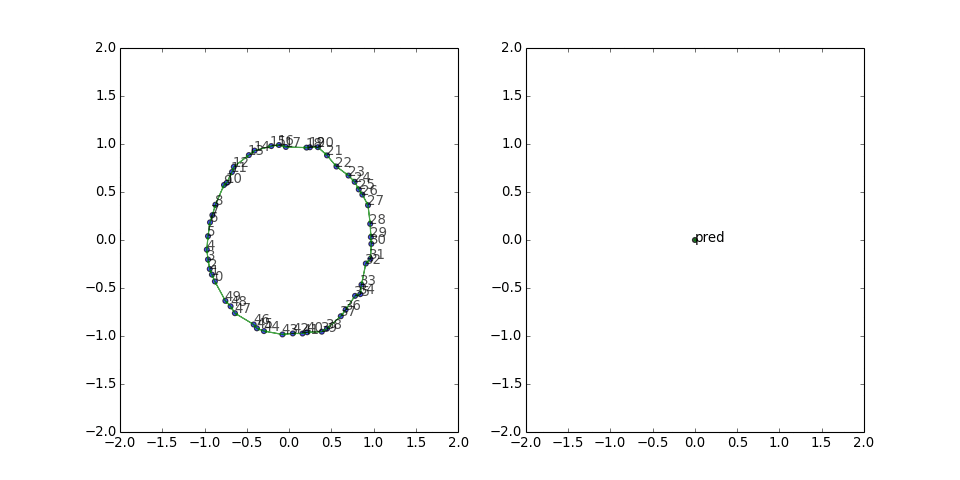
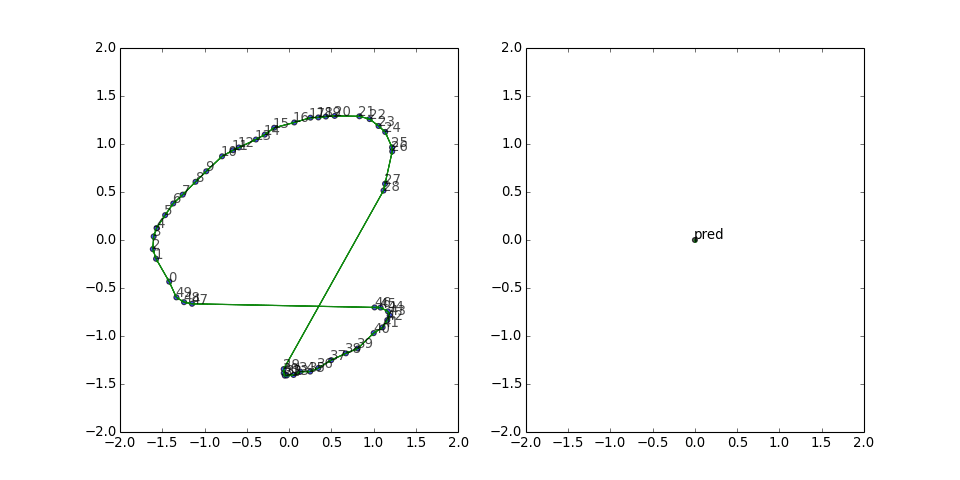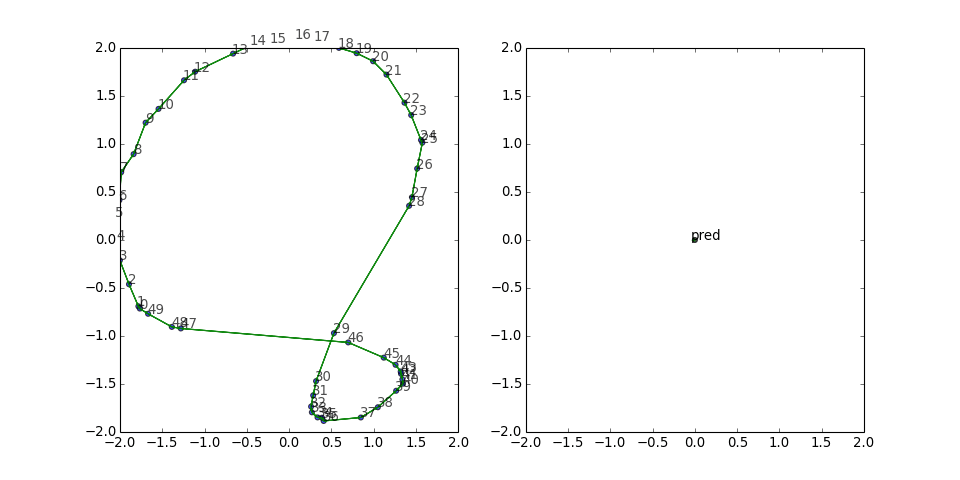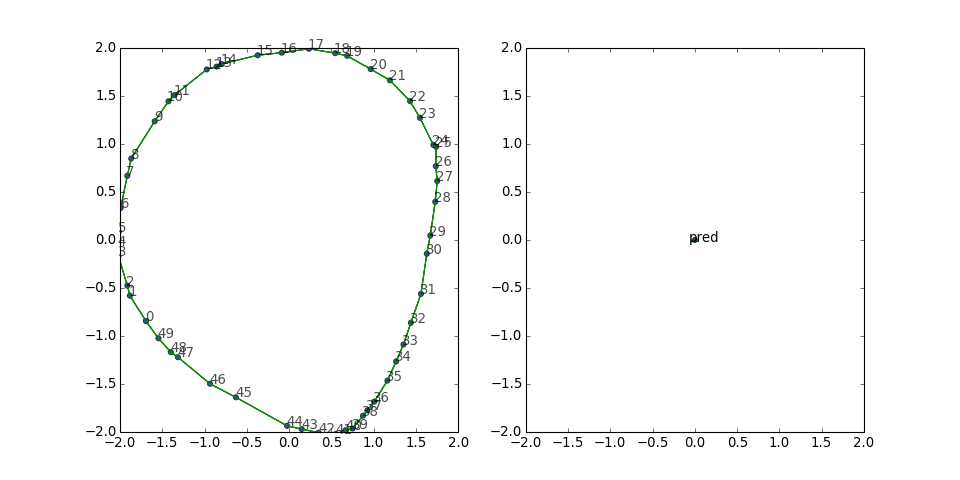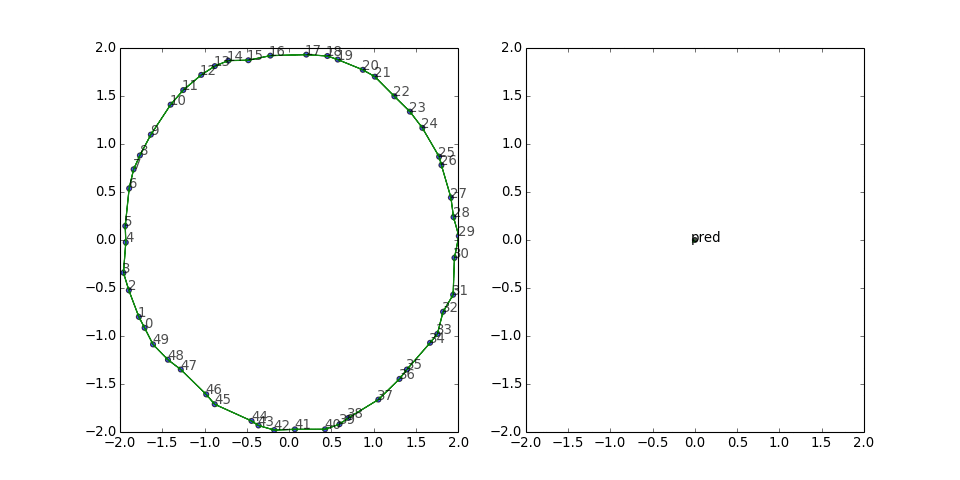
Cycle graph

Next I tried a cycle graph. As expected, the predicate vector goes to zero because it is getting translational updates from all different directions. Still, the layout works pretty well most of the time:

However, sometimes it has to work harder...

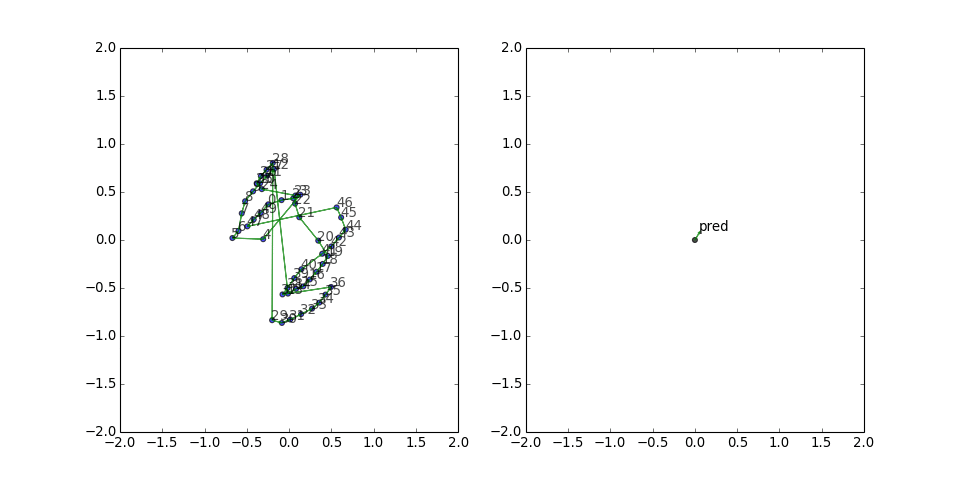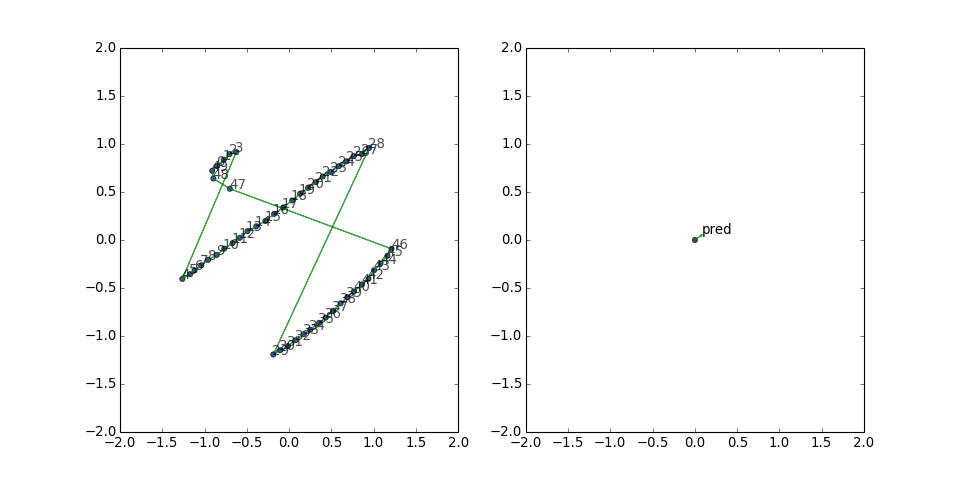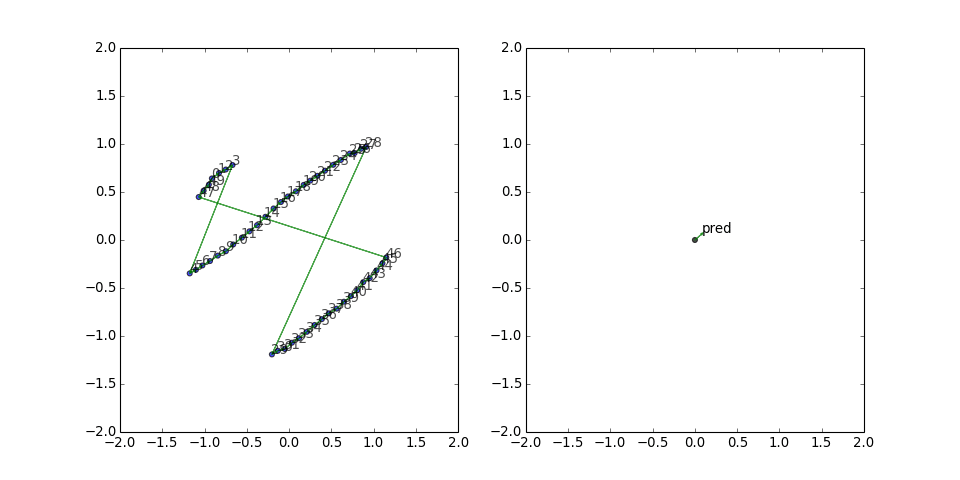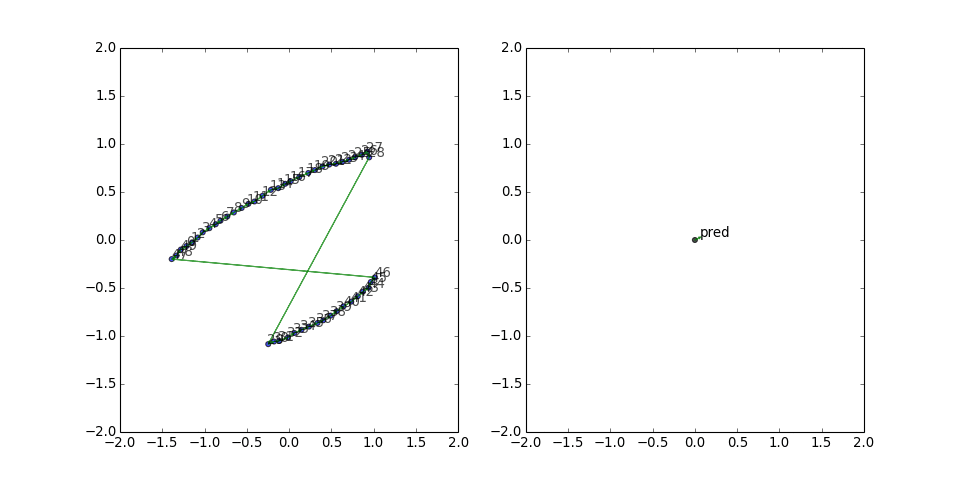
and still gets stuck:

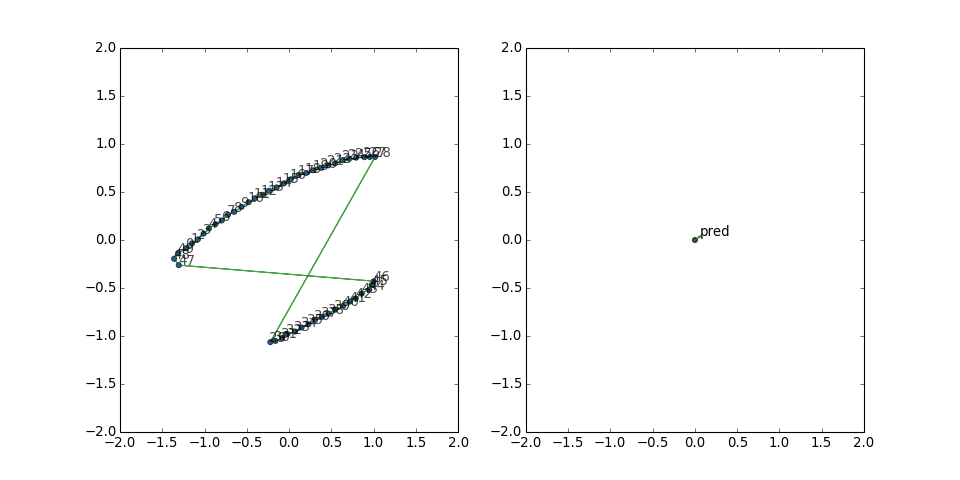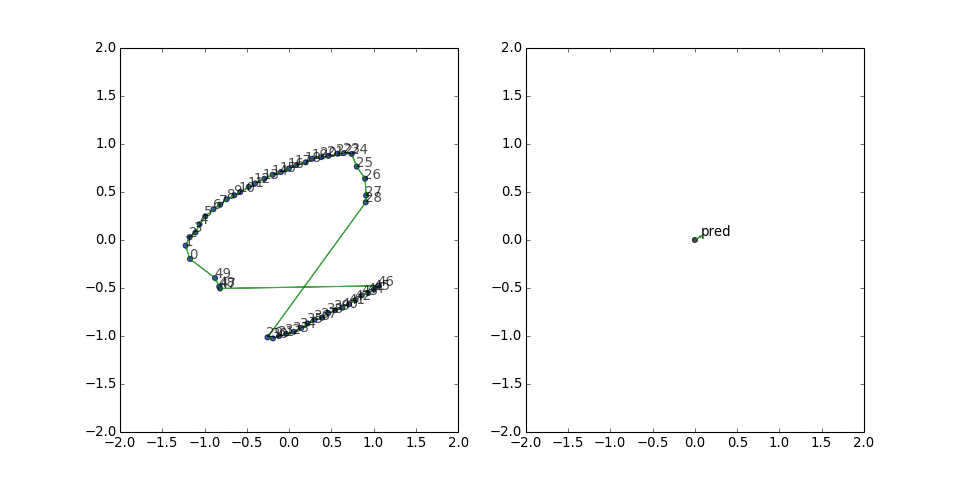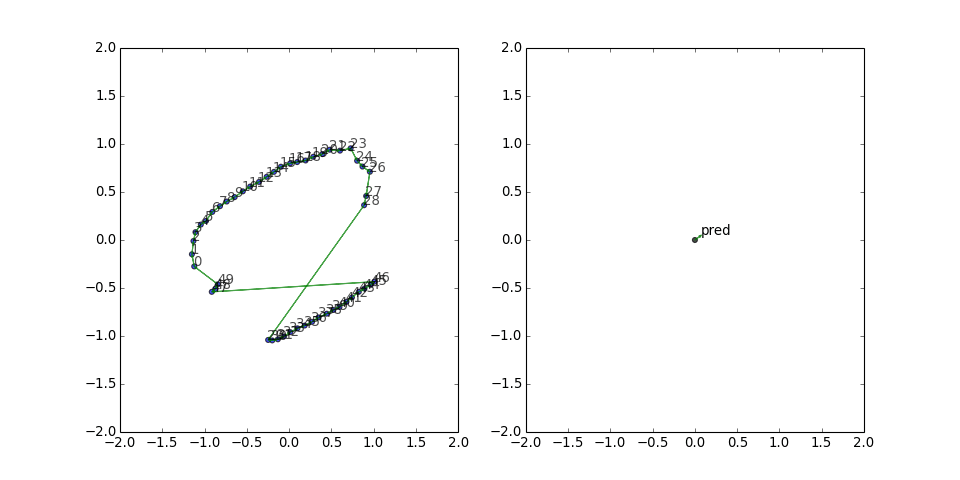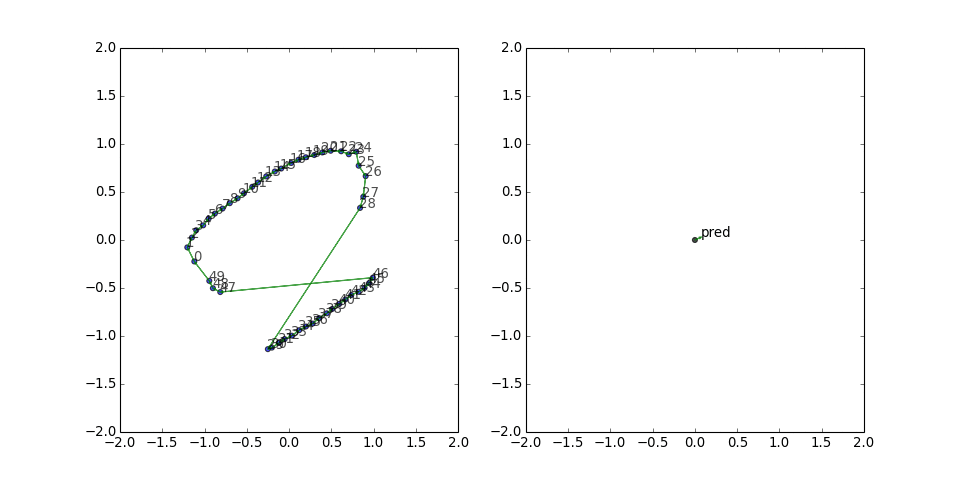
This figure-eight configuration seems to be a rather persistent local minimum for the loss function. The predicate vector is small but has a consistent direction, and the two gradient updates from the long edges keep canceling out. So I thought, what if we also include all the reversed edges, to give it a chance to build up some updates in the same direction?

Cycle graph (symmetric edges)

With the reversed edges, the predicate vector is no longer stuck in one direction, and the graph looks rounder and manages to wiggle out of the potential well more often:

This result indicates that it might be worthwhile to include the reverse triples during training, especially if the graph is sparse.

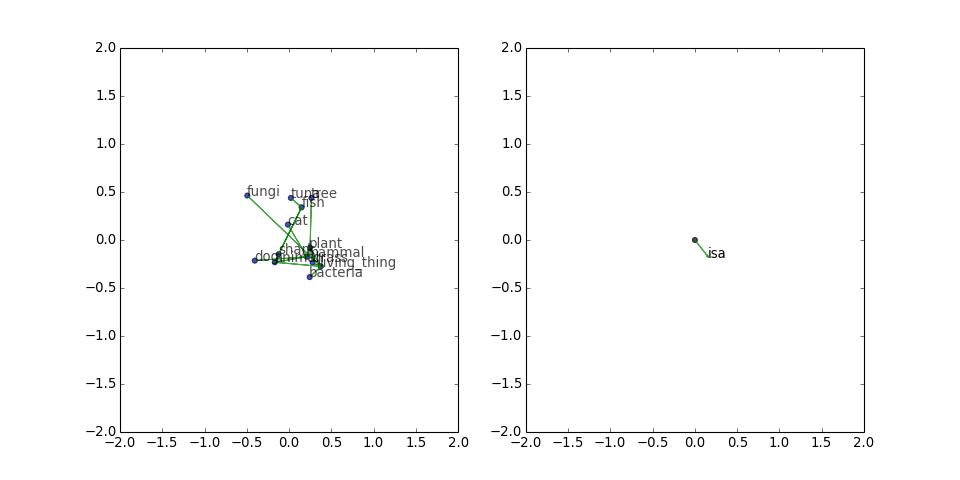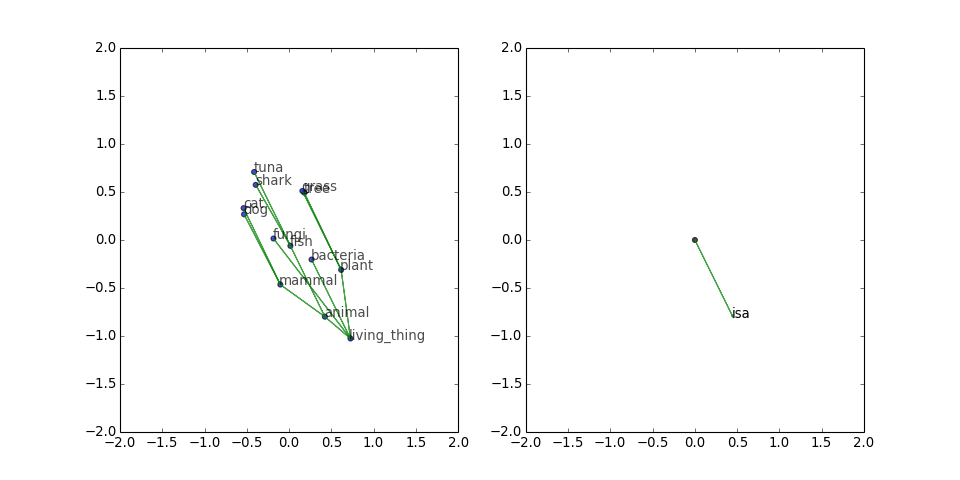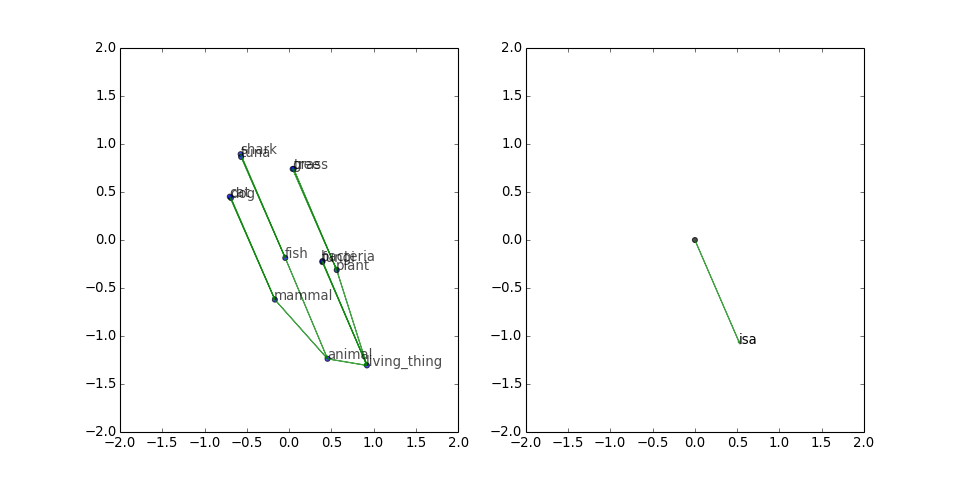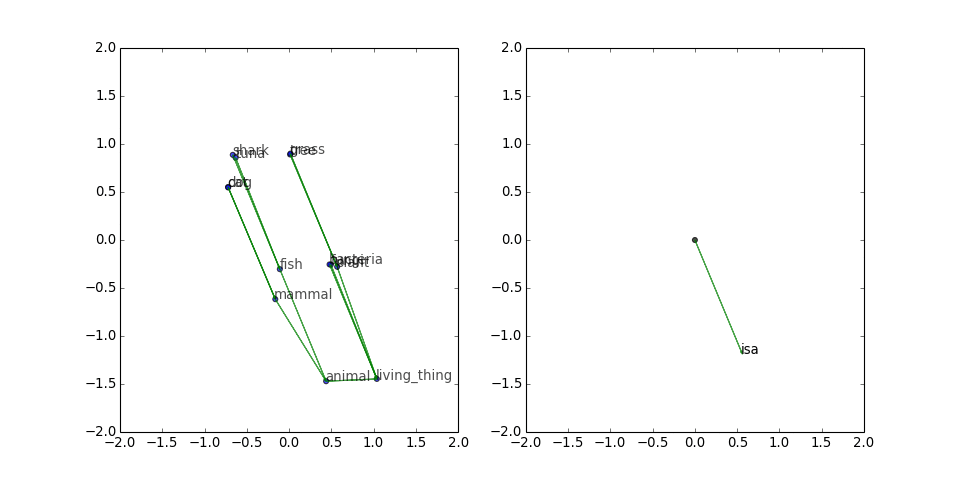
Tree

Next, I tried a small tree, with triples inspired by WordNet:

[('dog', 'isa', 'mammal'),  ('cat', 'isa', 'mammal'),  ('mammal', 'isa', 'animal'),  ('fish', 'isa', 'animal'),  ('shark', 'isa', 'fish'),  ('tuna', 'isa', 'fish'),  ('animal', 'isa', 'living_thing'),  ('bacteria', 'isa', 'living_thing'),  ('fungi', 'isa', 'living_thing'),  ('plant', 'isa', 'living_thing'),  ('tree', 'isa', 'plant'),  ('grass', 'isa', 'plant')]

TransE does an admirable job of drawing this tree, even though there is only one predicate. Note that the corruptions seem to provide repulsive forces that push the different branches apart, and these forces accumulate as you go toward the root.

Square grid

Next I tried a square grid with two predicates. The results look pretty good:

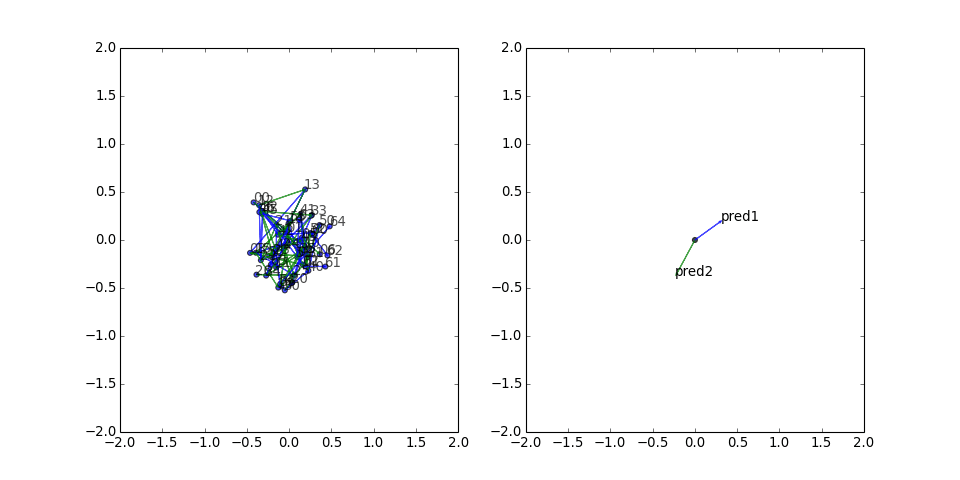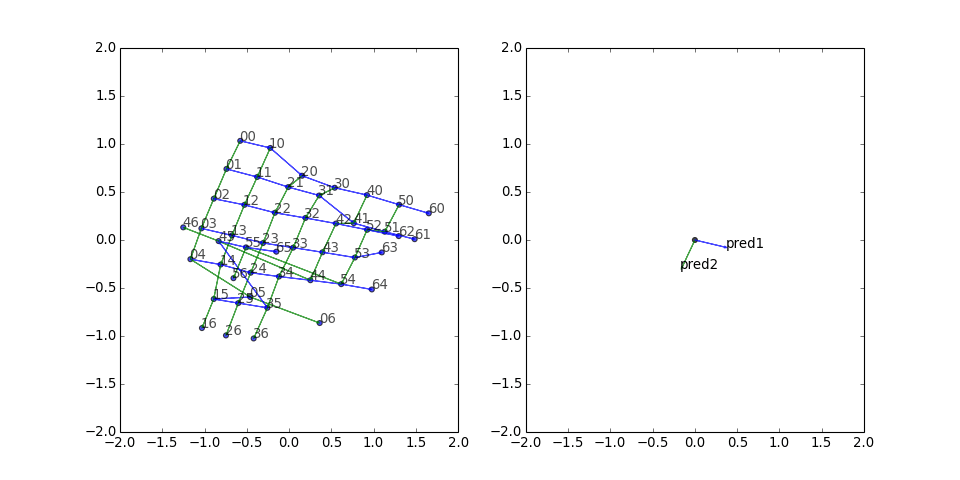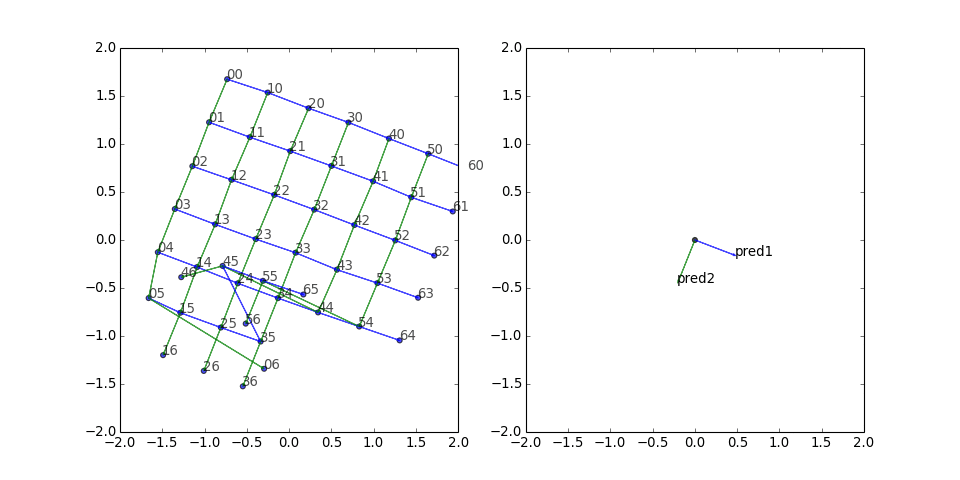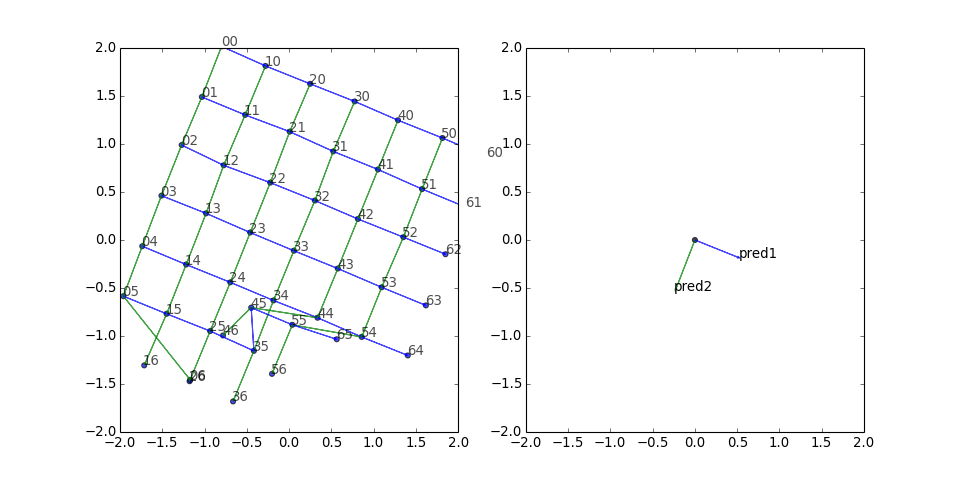
There seems to be a clump of five stragglers. What if we freeze the other vertices, turn off the corruptions, and just train those five?

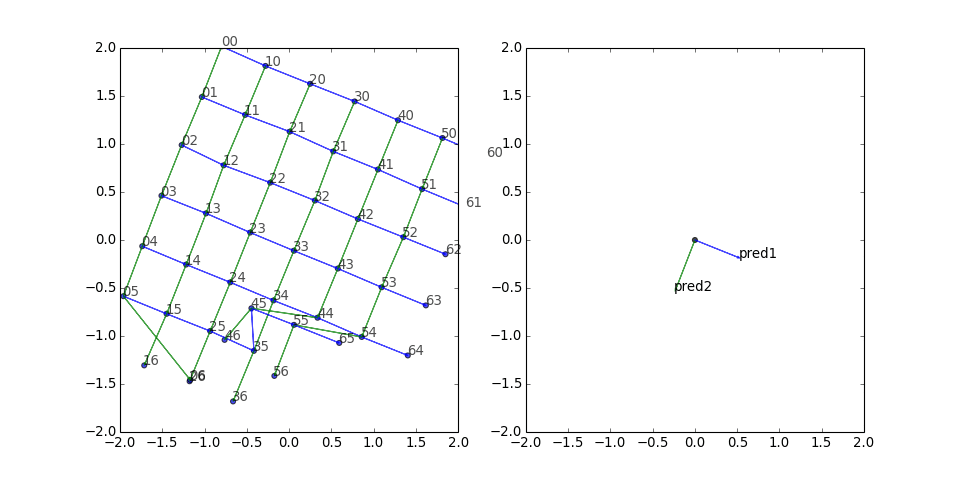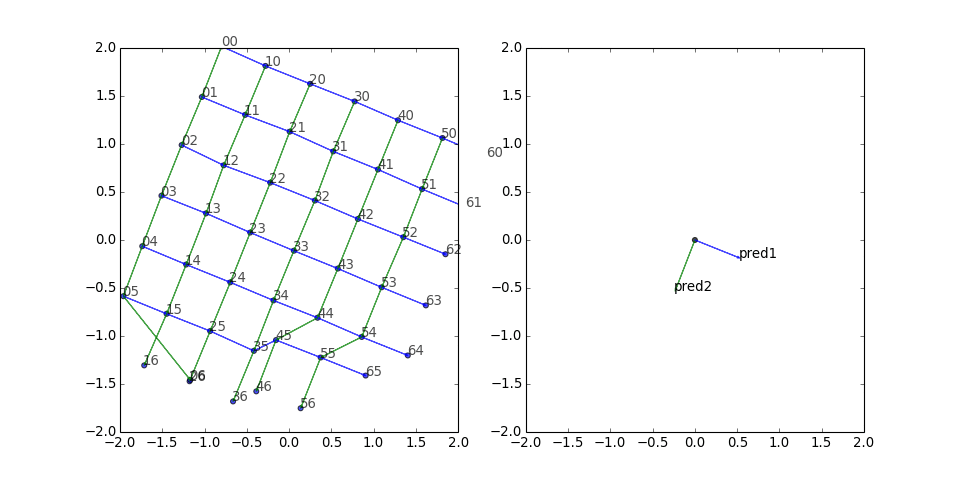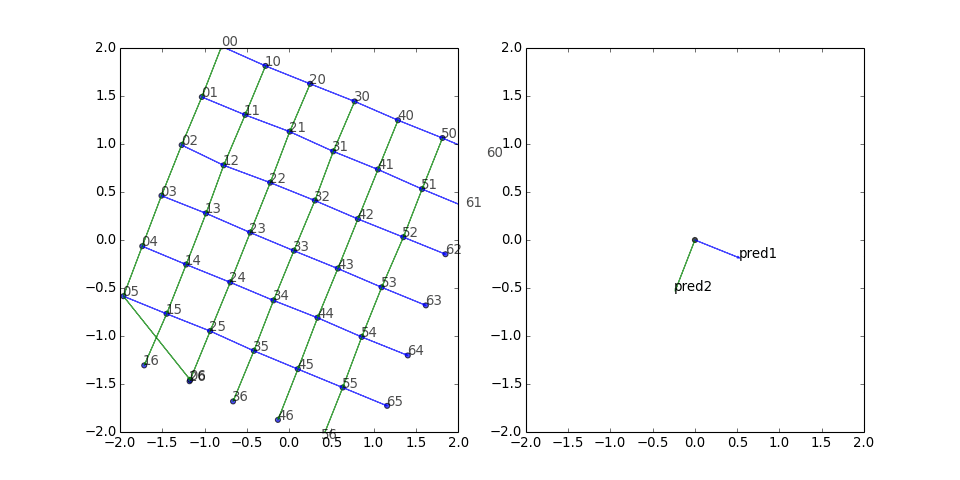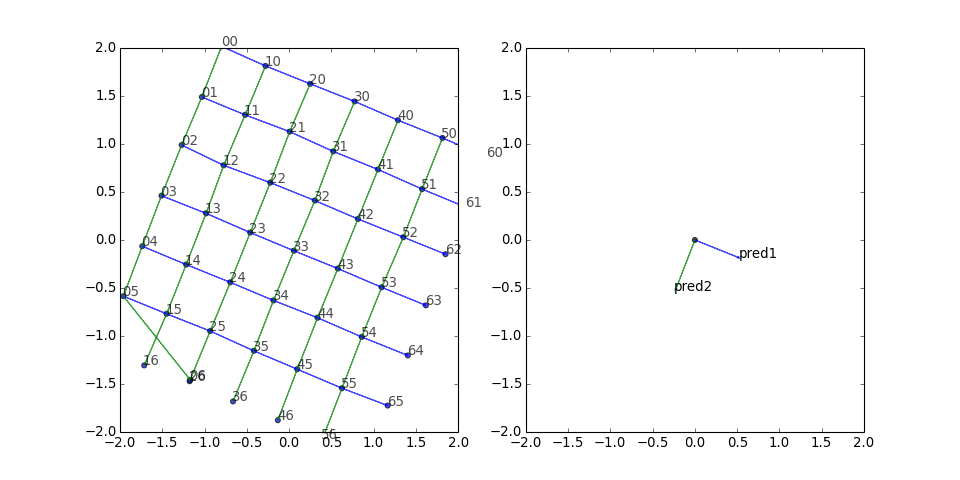
Nice—they find their way with only positive gradient updates. This looks encouraging for the insertion of new entities into the embedding space without retraining the whole thing.

In a future posting, we’ll look at what happens when a single predicate links a subject to many distinct objects, boolean attributes, three-dimensional embeddings, and the effect of various PyTorch optimizers on 3D embeddings.